Question
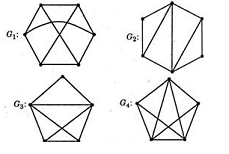
a.
G1
b.
G2
c.
G3
d.
G4
Posted under GATE cse question paper Engineering Mathematics
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. Which one of the following graphs is NOT planar ?
Similar Questions
Discover Related MCQs
Q. A binary operation on a set of integers is defined as x y = x^2 + y^2. Which one of the following statements is TRUE about ?
View solution
Q. Consider the set S = {1, ω, ω^2}, where ω and w^2 are cube roots of unity. If * denotes the multiplication operation, the structure (S, *) forms
View solution
Q. Which one of the following in NOT necessarily a property of a Group?
View solution
Q. Consider the binary relation R = {(x, y), (x, z), (z, x), (z, y)} on the set {x, y, z}. Which one of the following is TRUE?
View solution
Q. Let S be a set of n elements. The number of ordered pairs in the largest and the smallest equivalence relations on S are:
View solution
Q. How many different non-isomorphic Abelian groups of order 4 are there
View solution
Q. Let X, Y, Z be sets of sizes x, y and z respectively. Let W = X x Y. Let E be the set of all subsets of W. The number of functions from Z to E is:
View solution
Q. The set {1, 2, 3, 5, 7, 8, 9} under multiplication modulo 10 is not a group. Given below are four plausible reasons. Which one of them is false?
View solution
Q. A relation R is defined on ordered pairs of integers as follows: (x,y) R(u,v) if x < u and y > v. Then R is: Then R is:
View solution
Q. Let S denote the set of all functions f: {0,1}^4 -> {0,1}. Denote by N the number of functions from S to the set {0,1}. The value of Log2Log2N is ______.
View solution
Q. Consider the following relation on subsets of the set S of integers between 1 and 2014. For two distinct subsets U and V of S we say U < V if the minimum element in the symmetric difference of the two sets is in U. Consider the following two statements:
S1: There is a subset of S that is larger than every other subset.
S2: There is a subset of S that is smaller than every other subset.
Which one of the following is CORRECT?
View solution
Q. Let G be a group with 15 elements. Let L be a subgroup of G. It is known that L != G and that the size of L is at least 4. The size of L is __________.
View solution
Q. If V1 and V2 are 4-dimensional subspaces of a 6-dimensional vector space V, then the smallest possible dimension of V1 ∩ V2 is ______.
View solution
Q. There are two elements x, y in a group (G,∗) such that every element in the group can be written as a product of some number of x's and y's in some order. It is known that
x ∗ x = y ∗ y = x ∗ y ∗ x ∗ y = y ∗ x ∗ y ∗ x = e
where e is the identity element. The maximum number of elements in such a group is __________.
View solution
Q. Consider the set of all functions f: {0,1, … ,2014} → {0,1, … ,2014} such that f(f(i)) = i, for all 0 ≤ i ≤ 2014. Consider the following statements:
P. For each such function it must be the case that
for every i, f(i) = i.
Q. For each such function it must be the case that
for some i, f(i) = i.
R. Each such function must be onto.
Which one of the following is CORRECT?
View solution
Q. Let E, F and G be finite sets. Let X = (E ∩ F) - (F ∩ G) and Y = (E - (E ∩ G)) - (E - F). Which one of the following is true?
View solution
Q. Given a set of elements N = {1, 2, ..., n} and two arbitrary subsets A⊆N and B⊆N, how many of the n! permutations π from N to N satisfy min(π(A)) = min(π(B)), where min(S) is the smallest integer in the set of integers S, and π(S) is the set of integers obtained by applying permutation π to each element of S?
View solution
Q. Let A, B and C be non-empty sets and let X = (A - B) - C and Y = (A - C) - (B - C). Which one of the following is TRUE?
View solution
Q. The set {1, 2, 4, 7, 8, 11, 13, 14} is a group under multiplication modulo 15. The inverses of 4 and 7 are respectively
View solution
Q. Let R and S be any two equivalence relations on a non-empty set A. Which one of the following statements is TRUE?
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Engineering Mathematics? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!








