Question
a.
29
b.
31
c.
38
d.
41
Posted under GATE cse question paper Data Structures and Algorithms
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
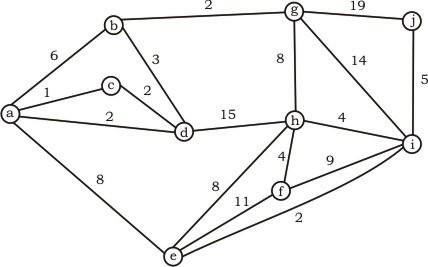
Q. What is the weight of a minimum spanning tree of the following graph ?
Similar Questions
Discover Related MCQs
Q. The following program fragment is written in a programming language that allows variables and does not allow nested declarations of functions.
global int i = 100, j = 5;
void P(x)
{
int i = 10;
print(x + 10);
i = 200;
j = 20;
print(x);
}
main()
{
P(i + j);
}
If the programming language uses static scoping and call by need parameter passing mechanism, the values printed by the above program are
View solution
Q. The following program fragment is written in a programming language that allows variables and does not allow nested declarations of functions.
global int i = 100, j = 5;
void P(x)
{
int i = 10;
print(x + 10);
i = 200;
j = 20;
print(x);
}
main()
{
P(i + j);
}
If the programming language uses dynamic scoping and call by name parameter passing mechanism, the values printed by the above program are :
View solution
Q. Consider the following class definitions in a hypothetical Object Oriented language that supports inheritance and uses dynamic binding. The language should not be assumed to be either Java or C++, though the syntax is similar.
Class P
{
void f(int i)
{
print(i);
}
}
Class Q subclass of P
{
void f(int i)
{
print(2*i);
}
}
Now consider the following program fragment:
P x = new Q();
Q y = new Q();
P z = new Q();
x.f(1); ((P)y).f(1); z.f(1);
Here ((P)y) denotes a typecast of y to P. The output produced by executing the above program fragment will be
View solution
Q. In the following C program fragment, j, k n and TwoLog_n are interger variables, and A is an array of integers. The variable n is initialized to an integer ≥ 3, and TwoLog_n is initialized to the value of 2*⌈log2(n)⌉
for (k = 3; k < = n; k++)
A[k] = 0;
for (k = 2; k < = TwoLog_n; k++)
for (j = k + 1; j < = n; j++)
A[j] = A[j] || (j % k);
for (j = 3; j < = n; j++)
if (!A[j]) printf("%d", j);
The set of numbers printed by this program fragment is
View solution
Q. Consider the C program shown below.
#define print(x) printf("%d ", x)
int x;
void Q(int z)
{
z += x;
print(z);
}
void P(int *y)
{
int x = *y + 2;
Q(x);
*y = x - 1;
print(x);
}
main(void)
{
x = 5;
P(&x);
print(x);
}
The output of this program is
View solution
Q. The goal of structured programming is to
View solution
Q. Consider the following C function
void swap (int a, int b)
{
int temp;
temp = a;
a = b;
b = temp;
}
In order to exchange the values of two variables x and y.
View solution
Q. The following numbers are inserted into an empty binary search tree in the given order: 10, 1, 3, 5, 15, 12, 16. What is the height of the binary search tree (the height is the maximum distance of a leaf node from the root)?
View solution
Q. The best data structure to check whether an arithmetic expression has balanced parentheses is a
View solution
Q. Consider the following C function:
int f(int n)
{
static int i = 1;
if (n >= 5)
return n;
n = n+i;
i++;
return f(n);
}
The value returned by f(1) is
View solution
Q. Consider the following program fragment for reversing the digits in a given integer to obtain a new integer. Let n = D1D2…Dm
int n, rev;
rev = 0;
while (n > 0)
{
rev = rev*10 + n%10;
n = n/10;
}
The loop invariant condition at the end of the ith iteration is:
View solution
Q. Consider the following C program segment:
char p[20];
char *s = "string";
int length = strlen(s);
int i;
for (i = 0; i < length; i++)
p[i] = s[length — i];
printf("%s",p);
The output of the program is
View solution
Q. Consider the label sequences obtained by the following pairs of traversals on a labeled binary tree. Which of these pairs identify a tree uniquely ?
(i) preorder and postorder
(ii) inorder and postorder
(iii) preorder and inorder
(iv) level order and postorder
View solution
Q. Two matrices M1 and M2 are to be stored in arrays A and B respectively. Each array can be stored either in row-major or column-major order in contiguous memory locations. The time complexity of an algorithm to compute M1 × M2 will be
View solution
Q. Consider the following C program
main()
{
int x, y, m, n;
scanf ("%d %d", &x, &y);
/* Assume x > 0 and y > 0 */
m = x;
n = y;
while (m! = n)
{
if (m > n)
m = m - n;
else
n = n - m;
}
print f ("% d", n);
}
The program computes
View solution
Q. What does the following algorithm approximate?
x = m;
y = 1;
while (x - y > e)
{
x = (x + y)/2;
y = m/x;
}
print(x);
(Assume m > 1, e > 0).
View solution
Q. Consider the following C program segment
struct CellNode
{
struct CelINode *leftchild;
int element;
struct CelINode *rightChild;
}
int Dosomething(struct CelINode *ptr)
{
int value = 0;
if (ptr != NULL)
{
if (ptr->leftChild != NULL)
value = 1 + DoSomething(ptr->leftChild);
if (ptr->rightChild != NULL)
value = max(value, 1 + DoSomething(ptr->rightChild));
}
return (value);
}
The value returned by the function DoSomething when a pointer to the root of a non-empty tree is passed as argument is
View solution
Q. The order of an internal node in a B+ tree index is the maximum number of children it can have. Suppose that a child pointer takes 6 bytes, the search field value takes 14 bytes, and the block size is 512 bytes. What is the order of the internal node?
View solution
Q. Let A[1, ..., n] be an array storing a bit (1 or 0) at each location, and f(m) is a unction whose time complexity is θ(m). Consider the following program fragment written in a C like language:
counter = 0;
for (i = 1; i < = n; i++)
{
if (A[i] == 1)
counter++;
else {
f(counter);
counter = 0;
}
}
The complexity of this program fragment is
View solution
Q. The time complexity of the following C function is (assume n > 0)
int recursive (int n) {
if (n == 1)
return (1);
else
return (recursive (n - 1) + recursive (n - 1));
}
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Data Structures and Algorithms? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!




.png)



