Question
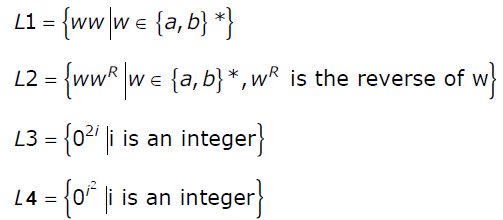
a.
Only L1 and L2
b.
Only L2, L3 and L4
c.
Only L3 and L4
d.
Only L3
Posted under GATE cse question paper Theory of Computation(TOC)
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. Consider the following languages. Which of the languages are regular?
Similar Questions
Discover Related MCQs
Q. Consider the following problem X.
Given a Turing machine M over the input alphabet Σ, any
state q of M And a word w∈Σ*, does the computation of M
on w visit the state q?
Which of the following statements about X is correct?
View solution
Q. The language accepted by a Pushdown Automation in which the stack is limited to 10 items is best described as
View solution
Q. Which of the following is true?
View solution
Q. The C language is:
View solution
Q. Ram and Shyam have been asked to show that a certain problem Π is NP-complete. Ram shows a polynomial time reduction from the 3-SAT problem to Π, and Shyam shows a polynomial time reduction from Π to 3-SAT. Which of the following can be inferred from these reductions ?
View solution
Q. Nobody knows yet if P = NP. Consider the language L defined as follows. Which of the following statements is true ?
View solution
Q. If the strings of a language L can be effectively enumerated in lexicographic (i.e., alphabetic) order, which of the following statements is true ?
View solution
Q. Let G = ({S}, {a, b} R, S) be a context free grammar where the rule set R is S → a S b | SS | ε . Which of the following statements is true?
View solution
Q. Define languages L0 and L1 as follows :
L0 = {< M, w, 0 > | M halts on w}
L1 = {< M, w, 1 > | M does not halts on w}
Here < M, w, i > is a triplet, whose first component. M is an encoding of a Turing Machine, second component, w, is a string, and third component, i, is a bit. Let L = L0 ∪ L1. Which of the following is true ?
View solution
Q. The language {a^m b^n C^(m+n) | m, n ≥ 1} is
View solution
Q. Consider the following grammar G:
S → bS | aA | b
A → bA | aB
B → bB | aS | a
Let Na(w) and Nb(w) denote the number of a's and b's in a string w respectively. The language L(G) ⊆ {a, b}+ generated by G is
View solution
Q. L1 is a recursively enumerable language over Σ. An algorithm A effectively enumerates its words as w1, w2, w3, ... Define another language L2 over Σ Union {#} as {wi # wj : wi, wj ∈ L1, i < j}. Here # is a new symbol. Consider the following assertions.
S1 : L1 is recursive implies L2 is recursive
S2 : L2 is recursive implies L1 is recursive
Which of the following statements is true ?
View solution
Q. Consider the languages L1 = {0^i1^j | i != j}. L2 = {0^i1^j | i = j}. L3 = {0^i1^j | i = 2j+1}. L4 = {0^i1^j | i != 2j}.
View solution
Q. S -> aSa|bSb|a|b; The language generated by the above grammar over the alphabet {a,b} is the set of
View solution
Q. The language L= {0^i21^i | i≥0 } over the alphabet {0,1, 2} is:
View solution
Q. Consider the CFG with {S,A,B) as the non-terminal alphabet, {a,b) as the terminal alphabet, S as the start symbol and the following set of production rules
S --> aB S --> bA
B --> b A --> a
B --> bS A --> aS
B --> aBB A --> bAA
Which of the following strings is generated by the grammar?
View solution
Q. Consider the following statements about the context free grammar
G = {S → SS, S → ab, S → ba, S → Ε}
I. G is ambiguous
II. G produces all strings with equal number of a’s and b’s
III. G can be accepted by a deterministic PDA.
Which combination below expresses all the true statements about G?
View solution
Q. Consider the languages:
L1 = {a^nb^nc^m | n, m > 0}
L2 = {a^nb^mc^m | n, m > 0}
Which one of the following statements is FALSE?
View solution
Q. Consider the languages:
L1 = {ww^R |w ∈ {0, 1}*}
L2 = {w#w^R | w ∈ {0, 1}*}, where # is a special symbol
L3 = {ww | w ∈ (0, 1}*)
Which one of the following is TRUE?
View solution
Q. Which of the following languages are context-free?
L1 = {a^m b^n a^n b^m ⎪ m, n ≥ 1}
L2 = {a^m b^n a^m b^n ⎪ m, n ≥ 1}
L3 = {a^m b^n ⎪ m = 2n + 1}
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Theory of Computation(TOC)? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!








