Question
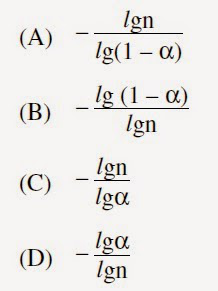
a.
A
b.
B
c.
C
d.
D
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. Suppose that the splits at every level of quicksort are in the proportion (1 – a) to a, where 0 < a ≤ ½ is a constant. The minimum depth of a leaf in the recursion tree is...
Similar Questions
Discover Related MCQs
Q. Suppose that the splits at every level of Quicksort are in proportion 1-β to β, where 0<β≤0.5 is a constant. The number of elements in an array is n. The maximum depth is approximately
View solution
Q. The minimum number of nodes in a binary tree of depth d (root is at level 0) is
View solution
Q. The efficient data structure to insert/delete a number in a stored set of numbers is
View solution
Q. Consider the following statements:
(i) A graph in which there is a unique path between every pair of vertices is a tree.
(ii) A connected graph with e = v – 1 is a tree.
(iii) A graph with e = v – 1 that has no circuit is a tree.
Which of the above statements is/are true?
View solution
Q. Consider the In-order and Post-order traversals of a tree as given below:
In-order: j e n k o p b f a c l g m d h i
Post-order: j n o p k e f b c l m g h i d a
The Pre-order traversal of the tree shall be
View solution
Q. A simple graph G with n-vertices is connected if the graph has
View solution
Q. Linked Lists are not suitable for ...................
View solution
Q. The decision tree classifier is a widely used technique for ...............
View solution
Q. Match the following :
(a) Dangling pointer (i) Buffer replacement policy
(b) Page fault (ii) Variable-length records
(c) List representation (iii) Object identifier
(d) Toss-immediate (iv) Pointer-swizzling
Codes :
(a) (b) (c) (d)
View solution
Q. The time complexity of recurrence relation
T(n) = T(n/3) + T(2n/3) + O(n)
is
View solution
Q. The time complexity of an efficient algorithm to find the longest monotonically increasing subsequence of n numbers is
View solution
Q. Given 0-1 knapsack problem and fractional knapsack problem and the following statements :
S1 : 0-1 knapsack is efficiently solved using Greedy algorithm.
S2 : Fractional knapsack is efficiently solved using Dynamic programming.
Which of the following is true ?
View solution
Q. Consider the following sequence of operations :
(i) Pointer p1 is set to point at a new heap-dynamic variable.
(ii) Pointer p2 is assigned p1’s value.
(iii) The heap dynamic variable pointed to by p1 is explicitly de-allocated, but p2 is not changed by the operation.
This situation leads to which of the following :
View solution
Q. Cyclometric complexity of a flow graph G with n vertices and e edges is
View solution
Q. For a B-tree of height h and degree t, the total CPU time used to insert a node is
View solution
Q. The time complexity to build a heap with a list of n numbers is
View solution
Q. The value of postfix expression:
8 3 4 + - 3 8 2 / + * 2 $ 3+ is
View solution
Q. Consider the following statements for priority queue:
S1: It is a data structure in which the intrinsic ordering of the elements does determine the result of its basic operations.
S2: The elements of a priority queue may be complex structures that are ordered on one or several fields.
Which of the following is correct?
View solution
Q. Give as good a big-O estimate as possible for the following functions:
(nlogn+n^2)(n^3+2) and (n!+2^n)(n^3+log(n^2+ 1))
View solution
Q. In any n-element heap, the number of nodes of height h is
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Data Structures and Algorithms? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!





.png)


