Question
impulse(1,[1 _], ‘red’);
hold on;
impulse(1,[1 a], ‘blue’);
impulse(1,[1 b], ‘yellow’);
impulse(1,[1 _], ‘green’);
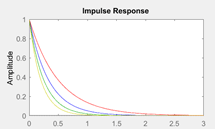
a.
a<b
b.
a>b
c.
a=b
d.
Cannot be determined
Posted under MATLAB
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. Choose the correct option after observing the given graph and the code snippet carefully. impulse(1,[1 _], ‘red’); hold on; impulse(1,[1 a], ‘blue’); impulse(1,[1 b],...
Similar Questions
Discover Related MCQs
Q. How does the pole of the transfer function change?
View solution
Q. What is the slope of the ramp function?
View solution
Q. What is the output at the scope?
View solution
Q. What does the following relate to?
View solution
Q. The default Laplace transform, of functions, computed by MATLAB is __________
View solution
Q. The laplace transform of step function, u(t), can be calculated by using _____
View solution
Q. The Transfer Function of an L.T.I. system is ___________
View solution
Q. The final value theorem is applicable if __________
View solution
Q. If f(t)=f₁(t)+f₂(t), the laplace transform of f(t) exists if f₁(t) and f₂(t) does not have the same R.O.C.
View solution
Q. What is the default variable used to represent the laplace transform in the output?
View solution
Q. A causal system is stable if the pole lies on the right half of the s-plane.
View solution
Q. An L.T.I. system is stable if _______
View solution
Q. The number of inverse lapalace transform of a function is equal to ________
View solution
Q. The laplace transform method used to solve a differential function is ____ than the classical way.
View solution
Q. The laplace transform of a cascaded system is defined if _______
View solution
Q. The inverse laplace transform of a function in s-domain is the transfer function of the system.
View solution
Q. The differential equation d2p/dt2=9t has a solution.
View solution
Q. The transient response, yt(t), of a system becomes ____ as t tends to infinity.
View solution
Q. The steady state value of a system is _____ it’s a transient response.
View solution
Q. Delay time is the time required by a system to reach a quarter of its steady state value.
View solution
Suggested Topics
Are you eager to expand your knowledge beyond MATLAB? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!

.png)






