Question
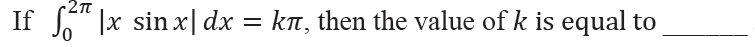
a.
2
b.
3
c.
4
d.
5
Posted under GATE cse question paper Engineering Mathematics
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. Consider the following statement :
Similar Questions
Discover Related MCQs
Q. Consider a function f(x) = 1 – |x| on –1 ≤ x ≤ 1. The value of x at which the function attains a maximum and the maximum value of the function are:
View solution
Q. Let f(x) = x^ –(1/3) and A denote the area of the region bounded by f(x) and the X-axis, when x varies from –1 to 1. Which of the following statements is/are True?
1. f is continuous in [–1, 1]
2. f is not bounded in [–1, 1]
3. A is nonzero and finite
View solution
Q. The velocity v (in kilometer/minute) of a motorbike which starts from rest, is given at fixed intervals of time t(in minutes) as follows:
t 2 4 6 8 10 12 14 16 18 20
v 10 18 25 29 32 20 11 5 2 0
The approximate distance (in kilometers) rounded to two places of decimals covered in 20 minutes using Simpson’s 1/3rd rule is _________.
View solution
Q. Let X and Y be two exponentially distributed and independent random variables with mean α and β, respectively. If Z = min(X,Y), then the mean of Z is given by
View solution
Q. If f(1) = 2,f(2) = 4 and f(4) = 16, what is the value of f(3)using Lagrange’s interpolation formula?
View solution
Q. Consider the following iterative root finding methods and convergence properties:
Iterative root finding Convergence properties methods
(Q) False Position (I) Order of convergence = 1.62
(R) Newton Raphson (II) Order of convergence = 2
(S) Secant (III) Order of convergence = 1 with guarantee of convergence
(T) Successive Approximation (IV) Order of convergence = 1 with no guarantee of convergence
View solution
Q. Let f(n), g(n) and h(n) be functions defined for positive inter such that f(n) = O(g(n)), g(n) ≠ O(f(n)), g(n) = O(h(n)), and h(n) = O(g(n)). Which one of the following statements is FALSE?
View solution
Q. Find the Integral value of f(x) = x * sinx within the limits 0, π.
View solution
Q. The value of the constant 'C' using Lagrange's mean value theorem for f(x) = 8x - x^2 in [0,8] is:
View solution
Q. Consider an undirected random graph of eight vertices. The probability that there is an edge between a pair of vertices is 1/2. What is the expected number of unordered cycles of length three?
View solution
Q. Which of the following statements is/are TRUE for undirected graphs?
P: Number of odd degree vertices is even.
Q: Sum of degrees of all vertices is even.
View solution
Q. The line graph L(G) of a simple graph G is defined as follows: · There is exactly one vertex v(e) in L(G) for each edge e in G. · For any two edges e and e' in G, L(G) has an edge between v(e) and v(e'), if and only if e and e'are incident with the same vertex in G. Which of the following statements is/are TRUE?
(P) The line graph of a cycle is a cycle.
(Q) The line graph of a clique is a clique.
(R) The line graph of a planar graph is planar.
(S) The line graph of a tree is a tree.
View solution
Q. Let G be a simple undirected planar graph on 10 vertices with 15 edges. If G is a connected graph, then the number of bounded faces in any embedding of G on the plane is equal to
View solution
Q. Let G be a complete undirected graph on 6 vertices. If vertices of G are labeled, then the number of distinct cycles of length 4 in G is equal to
View solution
Q. Let G = (V,E) be a graph. Define ξ(G) = Σd id x d, where id is the number of vertices of degree d in G. If S and T are two different trees with ξ(S) = ξ(T),then
View solution
Q. The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order. Which of the following sequences can not be the degree sequence of any graph?
I. 7, 6, 5, 4, 4, 3, 2, 1
II. 6, 6, 6, 6, 3, 3, 2, 2
III. 7, 6, 6, 4, 4, 3, 2, 2
IV. 8, 7, 7, 6, 4, 2, 1, 1
View solution
Q. What is the chromatic number of an n-vertex simple connected graph which does not contain any odd length cycle? Assume n >= 2.
View solution
Q. Which of the following statements is true for every planar graph on n vertices?
View solution
Q. Let G be the non-planar graph with the minimum possible number of edges. Then G has
View solution
Q. Which of the following graphs has an Eulerian circuit?
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Engineering Mathematics? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!








