Question
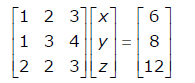
a.
x=6,y=3,z=2
b.
x=12,y=3,z=-4
c.
x=6,y=6,z=-4
d.
x=12,y=-3,z=0
Posted under GATE cse question paper Engineering Mathematics
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. What values of x, y and z satisfy the following system of linear equations?
Similar Questions
Discover Related MCQs
Q. Two eigenvalues of a 3 x 3 real matrix P are (2 + √ -1) and 3. The determinant of P is _____
View solution
Q. Let f (x) be a polynomial and g(x) = f (x) be its derivative. If the degree of (f(x) + f(−x)) is 10, then the degree of (g(x) − g(−x)) is _______________ .
View solution
Q. Consider the systems, each consisting of m linear equations in n variables.
I. If m < n, then all such systems have a solution
II. If m > n, then none of these systems has a solution
III. If m = n, then there exists a system which has a solution
Which one of the following is CORRECT?
View solution
Q. Suppose that the eigenvalues of matrix A are 1, 2, 4. The determinant of (A^−1)^T is _________
View solution
Q. Consider the function f(x) = sin(x) in the interval [π/4, 7π/4]. The number and location(s) of the local minima of this function are
View solution
Q. The bisection method is applied to compute a zero of the function f(x) = x^4 – x^3 – x^2 – 4 in the interval [1,9]. The method converges to a solution after _______ iterations.
View solution
Q. Newton-Raphson method is used to compute a root of the equation x^2-13=0 with 3.5 as the initial value. The approximation after one iteration is
View solution
Q. What is the value of Limn->∞(1-1/n)^2n ?
View solution
Q. Two alternative packages A and B are available for processing a database having 10k records.Package A requires 0.0001n^2 time units and package B requires 10nlog10n time units to process n records.What is the smallest value of k for which package B will be preferred over A?
View solution
Q. The minimum number of equal length subintervals needed to approximate the following expression to an accuracy of 1/3 * 10^-6 at least using the trapezoidal rule is
View solution
Q. A point on a curve is said to be an extremum if it is a local minimum or a local maximum. The number of distinct extrema for the curve 3x^4 - 16x^3 + 24x^2 + 37
View solution
Q. Consider the following two statements about the function f(x)=|x|
P. f(x) is continuous for all real values of x
Q. f(x) is differentiable for all real values of x
Which of the following is TRUE?
View solution
Q. Consider the series Xn+1 = Xn/2 + 9/(8 Xn), X0 = 0.5 obtained from the Newton-Raphson method. The series converges to
View solution
Q. Consider the polynomial p(x) = a0 + a1x + a2x^2 + a3x^3 , where ai ≠ 0 ∀i. The minimum number of multiplications needed to evaluate p on an input x is:
View solution
Q. Consider the following system of equations:
3x + 2y = 1
4x + 7z = 1
x + y + z = 3
x – 2y + 7z = 0
The number of solutions for this system is __________________
View solution
Q. The value of the dot product of the eigenvectors corresponding to any pair of different eigenvalues of a 4-by-4 symmetric positive definite matrix is _____________________.
View solution
Q. A non-zero polynomial f(x) of degree 3 has roots at x = 1, x = 2 and x = 3. Which one of the following must be TRUE?
View solution
Q. In the Newton-Raphson method, an initial guess of x0 = 2 is made and the sequence x0, x1, x2 … is obtained for the function
0.75x^3 – 2x^2 – 2x + 4 = 0
Consider the statements
(I) x3 = 0.
(II) The method converges to a solution in a finite number of iterations.
Which of the following is TRUE?
View solution
Q. Consider a function f(x) = 1 – |x| on –1 ≤ x ≤ 1. The value of x at which the function attains a maximum and the maximum value of the function are:
View solution
Q. Let f(x) = x^ –(1/3) and A denote the area of the region bounded by f(x) and the X-axis, when x varies from –1 to 1. Which of the following statements is/are True?
1. f is continuous in [–1, 1]
2. f is not bounded in [–1, 1]
3. A is nonzero and finite
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Engineering Mathematics? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!








