Question
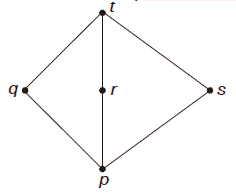
For any x, y ∈ L, not necessarily distinct, x ∨ y and x ∧ y are join and meet of x, y respectively. Let L^3 = {(x,y,z): x, y, z ∈ L} be the set of all ordered triplets of the elements of L. Let pr be the probability that an element (x,y,z) ∈ L^3 chosen equiprobably satisfies x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z). Then
a.
Pr = 0
b.
Pr = 1
c.
0 < Pr ≤ 1/5
d.
1/5 < Pr < 1
Posted under GATE cse question paper Engineering Mathematics
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. Suppose L = {p, q, r, s, t} is a lattice represented by the following Hasse diagram. For any x, y ∈ L, not necessarily distinct, x ∨ y and x ∧ y are join and meet of x, y...
Similar Questions
Discover Related MCQs
Q. The product of the non-zero eigenvalues of the matrix
1 0 0 0 1
0 1 1 1 0
0 1 1 1 0
0 1 1 1 0
1 0 0 0 1
is ______
View solution
Q. Which one of the following statements is TRUE about every n×n matrix with only real eigenvalues?
View solution
Q. Consider the following system of equations in three real variables x1, x2 and x3:
2x1 - x2 + 3x3 = 1
3x1- 2x2 + 5x3 = 2
-x1 + 4x2 + x3 = 3
This system of equations has
View solution
Q. Let A, B, C, D be n × n matrices, each with non-zero determinant. If ABCD = 1, then B^-1 is
View solution
Q. In the LU decomposition of the matrix,
| 2 2 |
| 4 9 |
if the diagonal elements of U are both 1, then the lower diagonal entry l22 of L is
View solution
Q. Consider the following 2 × 2 matrix A where two elements are unknown and are marked by a and b. The eigenvalues of this matrix are –1 and 7. What are the values of a and b?
A = | 1 4 |
| b a |
View solution
Q. The larger of the two eigenvalues of the matrix
⎡ 4 5 ⎤
⎣ 2 1 ⎦
is ____
View solution
Q. Perform the following operations on the matrix:
⎡ 3 4 45⎤
⎢ 7 8 105⎥
⎣13 2 195⎦
1. Add the third row to the second row.
2. Subtract the third column from the first column.
The determinant of the resultant matrix is _____________.
View solution
Q. If the following system has non-trivial solution,
px + qy + rz = 0
qx + ry + pz = 0
rx + py + qz = 0
then which one of the following options is True?
View solution
Q. Let a(x, y), b(x, y,) and c(x, y) be three statements with variables x and y chosen from some universe. Consider the following statement:
(∃x)(∀y)[(a(x, y) ∧ b(x, y)) ∧ ¬c(x, y)]
Which one of the following is its equivalent?
View solution
Q. Two eigenvalues of a 3 x 3 real matrix P are (2 + √ -1) and 3. The determinant of P is _____
View solution
Q. Let f (x) be a polynomial and g(x) = f (x) be its derivative. If the degree of (f(x) + f(−x)) is 10, then the degree of (g(x) − g(−x)) is _______________ .
View solution
Q. Consider the systems, each consisting of m linear equations in n variables.
I. If m < n, then all such systems have a solution
II. If m > n, then none of these systems has a solution
III. If m = n, then there exists a system which has a solution
Which one of the following is CORRECT?
View solution
Q. Suppose that the eigenvalues of matrix A are 1, 2, 4. The determinant of (A^−1)^T is _________
View solution
Q. Consider the function f(x) = sin(x) in the interval [π/4, 7π/4]. The number and location(s) of the local minima of this function are
View solution
Q. The bisection method is applied to compute a zero of the function f(x) = x^4 – x^3 – x^2 – 4 in the interval [1,9]. The method converges to a solution after _______ iterations.
View solution
Q. Newton-Raphson method is used to compute a root of the equation x^2-13=0 with 3.5 as the initial value. The approximation after one iteration is
View solution
Q. What is the value of Limn->∞(1-1/n)^2n ?
View solution
Q. Two alternative packages A and B are available for processing a database having 10k records.Package A requires 0.0001n^2 time units and package B requires 10nlog10n time units to process n records.What is the smallest value of k for which package B will be preferred over A?
View solution
Q. The minimum number of equal length subintervals needed to approximate the following expression to an accuracy of 1/3 * 10^-6 at least using the trapezoidal rule is
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Engineering Mathematics? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!








