Question
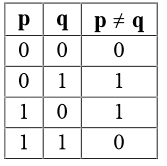
a.
Both commutative and associative
b.
Commutative but not associative
c.
Not commutative but associative
d.
Neither commutative nor associative
Posted under GATE cse question paper Engineering Mathematics
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. The binary operator ≠ is defined by the following truth table. Which one of the following is true about the binary operator ≠?
Similar Questions
Discover Related MCQs
Q. The product of the non-zero eigenvalues of the matrix
1 0 0 0 1
0 1 1 1 0
0 1 1 1 0
0 1 1 1 0
1 0 0 0 1
is ______
View solution
Q. Which one of the following statements is TRUE about every n×n matrix with only real eigenvalues?
View solution
Q. Consider the following system of equations in three real variables x1, x2 and x3:
2x1 - x2 + 3x3 = 1
3x1- 2x2 + 5x3 = 2
-x1 + 4x2 + x3 = 3
This system of equations has
View solution
Q. Let A, B, C, D be n × n matrices, each with non-zero determinant. If ABCD = 1, then B^-1 is
View solution
Q. In the LU decomposition of the matrix,
| 2 2 |
| 4 9 |
if the diagonal elements of U are both 1, then the lower diagonal entry l22 of L is
View solution
Q. Consider the following 2 × 2 matrix A where two elements are unknown and are marked by a and b. The eigenvalues of this matrix are –1 and 7. What are the values of a and b?
A = | 1 4 |
| b a |
View solution
Q. The larger of the two eigenvalues of the matrix
⎡ 4 5 ⎤
⎣ 2 1 ⎦
is ____
View solution
Q. Perform the following operations on the matrix:
⎡ 3 4 45⎤
⎢ 7 8 105⎥
⎣13 2 195⎦
1. Add the third row to the second row.
2. Subtract the third column from the first column.
The determinant of the resultant matrix is _____________.
View solution
Q. If the following system has non-trivial solution,
px + qy + rz = 0
qx + ry + pz = 0
rx + py + qz = 0
then which one of the following options is True?
View solution
Q. Let a(x, y), b(x, y,) and c(x, y) be three statements with variables x and y chosen from some universe. Consider the following statement:
(∃x)(∀y)[(a(x, y) ∧ b(x, y)) ∧ ¬c(x, y)]
Which one of the following is its equivalent?
View solution
Q. Two eigenvalues of a 3 x 3 real matrix P are (2 + √ -1) and 3. The determinant of P is _____
View solution
Q. Let f (x) be a polynomial and g(x) = f (x) be its derivative. If the degree of (f(x) + f(−x)) is 10, then the degree of (g(x) − g(−x)) is _______________ .
View solution
Q. Consider the systems, each consisting of m linear equations in n variables.
I. If m < n, then all such systems have a solution
II. If m > n, then none of these systems has a solution
III. If m = n, then there exists a system which has a solution
Which one of the following is CORRECT?
View solution
Q. Suppose that the eigenvalues of matrix A are 1, 2, 4. The determinant of (A^−1)^T is _________
View solution
Q. Consider the function f(x) = sin(x) in the interval [π/4, 7π/4]. The number and location(s) of the local minima of this function are
View solution
Q. The bisection method is applied to compute a zero of the function f(x) = x^4 – x^3 – x^2 – 4 in the interval [1,9]. The method converges to a solution after _______ iterations.
View solution
Q. Newton-Raphson method is used to compute a root of the equation x^2-13=0 with 3.5 as the initial value. The approximation after one iteration is
View solution
Q. What is the value of Limn->∞(1-1/n)^2n ?
View solution
Q. Two alternative packages A and B are available for processing a database having 10k records.Package A requires 0.0001n^2 time units and package B requires 10nlog10n time units to process n records.What is the smallest value of k for which package B will be preferred over A?
View solution
Q. The minimum number of equal length subintervals needed to approximate the following expression to an accuracy of 1/3 * 10^-6 at least using the trapezoidal rule is
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Engineering Mathematics? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!








