Question
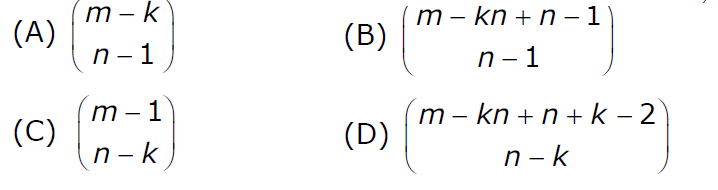
a.
A
b.
B
c.
C
d.
D
Posted under GATE cse question paper Engineering Mathematics
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. m identical balls are to be placed in n distinct bags. You are given that m ≥ kn, where, k is a natural number ≥ 1. In how many ways can the balls be placed in the bags if each bag...
Similar Questions
Discover Related MCQs
Q. Let f : A → B be an injective (one-to-one) function.
Define g : 2^A → 2^B as :
g(C) = {f(x) | x ∈ C}, for all subsets C of A.
Define h : 2^B → 2^A as :
h(D) = {x | x ∈ A, f(x) ∈ D}, for all subsets D of B.
Which of the following statements is always true ?
View solution
Q. Consider the set {a, b, c} with binary operators + and × defined as follows :
+ a b c × a b c
a b a c a a b c
b a b c b b c a
c a c b c c c b
For example, a + c = c, c + a = a, c × b = c and b × c = a. Given the following set of equations :
(a × x) + (a × y) = c
(b × x) + (c × y) = c
The number of solution(s) (i.e., pair(s) (x, y)) that satisfy the equations is :
View solution
Q. Consider two languages L1 and L2 each on the alphabet ∑. Let f : ∑ → ∑ be a polynomial time computable bijection such that (∀ x) [x ∈ L1 iff f(x) ∈ L2]. Further, let f^-1 be also polynomial time computable. Which of the following CANNOT be true?
View solution
Q. In a permutation a1.....an of n distinct integers, an inversion is a pair (ai, aj) such that i < j and ai > aj. If all permutations are equally likely, what is the expected number of inversions in a randomly chosen permutation of 1.....n ?
View solution
Q. In a permutation a1.....an of n distinct integers, an inversion is a pair (ai, aj) such that i < j and ai > aj. What would be the worst case time complexity of the Insertion Sort algorithm, if the inputs are restricted to permutations of 1.....n with at most n inversions?
View solution
Q. The cube root of a natural number n is defined as the largest natural number m such that m^3 ≤ n. The complexity of computing the cube root of n (n is represented in binary notation) is:
View solution
Q. The following resolution rule is used in logic programming:
Derive clause (P v Q) from clauses (P v R), (Q v ¬ R)
Which of the following statements related to this rule is FALSE?
View solution
Q. Identify the correct translation into logical notation of the following assertion.
"Some boys in the class are taller than all the girls"
Note : taller(x,y) is true if x is taller than y.
View solution
Q. If a fair coin is tossed four times. What is the probability that two heads and two tails will result?
View solution
Q. The number of different n × n symmetric matrices with each element being either 0 or 1 is:
(Note: power(2, x) is same as 2x)
View solution
Q. Let A, B, C, D be n × n matrices, each with non-zero determinant. If ABCD = 1, then B-1 is
View solution
Q. What is the result of evaluating the following two expressions using three-digit floating point arithmetic with rounding?
(113. + -111.) + 7.51
113. + (-111. + 7.51)
View solution
Q. The tightest lower bound on the number of comparisons, in the worst case, for comparison-based sorting is of the order of
View solution
Q. The problems 3-SAT and 2-SAT are
View solution
Q. The following propositional statement is
(P → (Q v R)) → ((P ^ Q) → R)
View solution
Q. How many solutions does the following system of linear equations have ?
-x + 5y = -1
x - y = 2
x + 3y = 3
View solution
Q. An examination paper has 150 multiple-choice questions of one mark each, with each question having four choices. Each incorrect answer fetches -0.25 mark. Suppose 1000 students choose all their answers randomly with uniform probability. The sum total of the expected marks obtained by all these students is:
View solution
Q. Mala has a colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour-pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement ?
View solution
Q. In an M'N matrix such that all non-zero entries are covered in a rows and b columns. Then the maximum number of non-zero entries, such that no two are on the same row or column, is
View solution
Q. Two n bit binary strings, S1 and S2, are chosen randomly with uniform probability. The probability that the Hamming distance between these strings (the number of bit positions where the two strings differ) is equal to d is
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Engineering Mathematics? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!








