Question
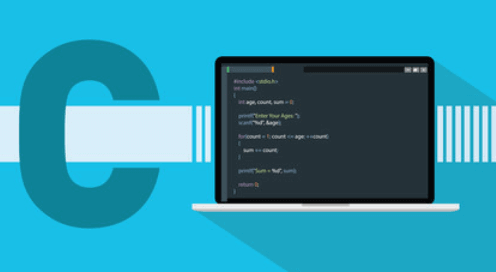
#include<stdio.h>
int main()
{
int arr[1000] = {-2, -5, 6, -2, 3, -1, 0,-5, 6}, len = 9;
int cur_max, tmp_max, strt_idx, sub_arr_idx;
cur_max = arr[0];
for(strt_idx = 0; strt_idx < len; strt_idx++)
{
tmp_max = 0;
for(sub_arr_idx = strt_idx; sub_arr_idx < len; sub_arr_idx++)
{
tmp_max += arr[sub_arr_idx];
if(tmp_max > cur_max)
cur_max = tmp_max;
}
}
printf("%d",cur_max);
return 0;
}
a.
6
b.
9
c.
7
d.
None of the mentioned
Posted under Data Structures and Algorithms
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. What is the output of the following naive method used to find the maximum sub-array sum?
Similar Questions
Discover Related MCQs
Q. What is the time complexity of the divide and conquer algorithm used to find the maximum sub-array sum?
View solution
Q. What is the space complexity of the divide and conquer algorithm used to find the maximum sub-array sum?
View solution
Q. Find the maximum sub-array sum for the following array:
{3, 6, 7, 9, 3, 8}
View solution
Q. Kadane’s algorithm is used to find ____________
View solution
Q. Kadane’s algorithm uses which of the following techniques?
View solution
Q. For which of the following inputs would Kadane’s algorithm produce the CORRECT output?
View solution
Q. For which of the following inputs would Kadane’s algorithm produce a WRONG output?
View solution
Q. What is the time complexity of Kadane’s algorithm?
View solution
Q. What is the space complexity of Kadane’s algorithm?
View solution
Q. The longest increasing subsequence problem is a problem to find the length of a subsequence from a sequence of array elements such that the subsequence is sorted in increasing order and it’s length is maximum. This problem can be solved using __________
View solution
Q. Find the longest increasing subsequence for the given sequence:
{10, -10, 12, 9, 10, 15, 13, 14}
View solution
Q. Find the length of the longest increasing subsequence for the given sequence:
{-10, 24, -9, 35, -21, 55, -41, 76, 84}
View solution
Q. For any given sequence, there will ALWAYS be a unique increasing subsequence with the longest length.
View solution
Q. The number of increasing subsequences with the longest length for the given sequence are:
{10, 9, 8, 7, 6, 5}
View solution
Q. In the brute force implementation to find the longest increasing subsequence, all the subsequences of a given sequence are found. All the increasing subsequences are then selected and the length of the longest subsequence is found. What is the time complexity of this brute force implementation?
View solution
Q. Given a rod of length n and the selling prices of all pieces smaller than equal to n, find the most beneficial way of cutting the rod into smaller pieces. This problem is called the rod cutting problem. Which of these methods can be used to solve the rod cutting problem?
View solution
Q. You are given a rod of length 5 and the prices of each length are as follows:
length price
1 2
2 5
3 6
4 9
5 9
What is the maximum value that you can get after cutting the rod and selling the pieces?
View solution
Q. Consider the brute force implementation of the rod cutting problem in which all the possible cuts are found and the maximum value is calculated. What is the time complexity of this brute force implementation?
View solution
Q. You are given a rod of length 10 and the following prices.
length price
1 2
2 5
3 6
4 9
5 9
6 17
7 17
8 18
9 20
10 22
Which of these pieces give the maximum price?
View solution
Q. For every rod cutting problem there will be a unique set of pieces that give the maximum price.
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Data Structures and Algorithms? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!