Question
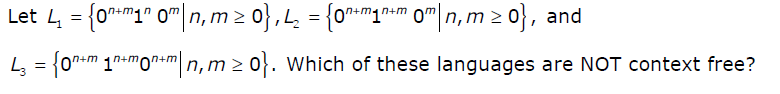
a.
L1 only
b.
L3 Only
c.
L1 and L2
d.
L2 and L3
Posted under GATE cse question paper Theory of Computation(TOC)
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. Consider the below statement:
Similar Questions
Discover Related MCQs
Q. Consider the following statements about the context free grammar
G = {S → SS, S → ab, S → ba, S → Ε}
I. G is ambiguous
II. G produces all strings with equal number of a’s and b’s
III. G can be accepted by a deterministic PDA.
Which combination below expresses all the true statements about G?
View solution
Q. Consider the languages:
L1 = {a^nb^nc^m | n, m > 0}
L2 = {a^nb^mc^m | n, m > 0}
Which one of the following statements is FALSE?
View solution
Q. Consider the languages:
L1 = {ww^R |w ∈ {0, 1}*}
L2 = {w#w^R | w ∈ {0, 1}*}, where # is a special symbol
L3 = {ww | w ∈ (0, 1}*)
Which one of the following is TRUE?
View solution
Q. Which of the following languages are context-free?
L1 = {a^m b^n a^n b^m ⎪ m, n ≥ 1}
L2 = {a^m b^n a^m b^n ⎪ m, n ≥ 1}
L3 = {a^m b^n ⎪ m = 2n + 1}
View solution
Q. Which one of the following statements is FALSE ?
View solution
Q. Consider the pushdown automaton (PDA) below which runs over the input alphabet (a, b, c). It has the stack alphabet {Z0, X} where Z0 is the bottom-of-stack marker. The set of states of the PDA is (s, t, u, f} where s is the start state and f is the final state. The PDA accepts by final state. The transitions of the PDA given below are depicted in a standard manner. For example, the transition (s, b, X) → (t, XZ0) means that if the PDA is in state s and the symbol on the top of the stack is X, then it can read b from the input and move to state t after popping the top of stack and pushing the symbols Z0 and X (in that order) on the stack.
(s, a, Z0) → (s, XXZ0)
(s, ϵ, Z0) → (f, ϵ)
(s, a, X) → (s, XXX)
(s, b, X) → (t, ϵ)
(t, b, X) → (t,.ϵ)
(t, c, X) → (u, ϵ)
(u, c, X) → (u, ϵ)
(u, ϵ, Z0) → (f, ϵ)
The language accepted by the PDA is
View solution
Q. A CFG G is given with the following productions where S is the start symbol, A is a non-terminal and a and b are terminals.
S→aS∣A
A→aAb∣bAa∣ϵ
Which of the following strings is generated by the grammar above?
View solution
Q. Consider 2 scenarios:
C1: For DFA (ϕ, Ʃ, δ, qo, F),
if F = ϕ, then L = Ʃ*
C2: For NFA (ϕ, Ʃ, δ, qo, F),
if F = ϕ, then L = Ʃ*
Where F = Final states set
ϕ = Total states set
Choose the correct option ?
View solution
Q. Let G be the CFG, l be the number of left most derivations, r be the number of right most derivations and P be the number of parse trees. Assume l , r and P are computed for a particular string. For a given CFG ‘G’ and given string ‘w’, what is the relation between l , P , r ?
View solution
Q. Which of the following statements is/are FALSE?
1. For every non-deterministic Turing machine,
there exists an equivalent deterministic Turing machine.
2. Turing recognizable languages are closed under union
and complementation.
3. Turing decidable languages are closed under intersection
and complementation.
4. Turing recognizable languages are closed under union
and intersection.
View solution
Q. Let L1 be a recursive language. Let L2 and L3 be languages that are recursively enumerable but not recursive. Which of the following statements is not necessarily true?
(A) L2 – L1 is recursively enumerable.
(B) L1 – L3 is recursively enumerable
(C) L2 ∩ L1 is recursively enumerable
(D) L2 ∪ L1 is recursively enumerable.
View solution
Q. If L and L' are recursively enumerable, then L is
View solution
Q. Let L be a language and L' be its complement. Which one of the following is NOT a viable possibility?
View solution
Q. Let A ≤m B denotes that language A is mapping reducible (also known as many-to-one reducible) to language B. Which one of the following is FALSE?
View solution
Q. For S ∈ (0 + 1) * let d(s) denote the decimal value of s (e.g. d(101) = 5). Let L = {s ∈ (0 + 1)* d(s)mod5 = 2 and d(s)mod7 != 4}. Which one of the following statements is true?
View solution
Q. Let L1 be a recursive language, and let L2 be a recursively enumerable but not a recursive language. Which one of the following is TRUE?
L1' --> Complement of L1
L2' --> Complement of L2
View solution
Q. A single tape Turing Machine M has two states q0 and q1, of which q0 is the starting state. The tape alphabet of M is {0, 1, B} and its input alphabet is {0, 1}. The symbol B is the blank symbol used to indicate end of an input string. The transition function of M is described in the following table
0 1 B
q0 q1, 1, R q1, 1, R Halt
q1 q1, 1, R q0, 1, L q0, B, L
The table is interpreted as illustrated below. The entry (q1, 1, R) in row q0 and column 1 signifies that if M is in state q0 and reads 1 on the current tape square, then it writes 1 on the same tape square, moves its tape head one position to the right and transitions to state q1. Which of the following statements is true about M ?
View solution
Q. For any two languages L1 and L2 such that L1 is context free and L2 is recursively enumerable but not recursive, which of the following is/are necessarily true?
1. L1' (complement of L1) is recursive
2. L2' (complement of L2) is recursive
3. L1' is context-free
4. L1' ∪ L2 is recursively enumerable
View solution
Q. Let X be a recursive language and Y be a recursively enumerable but not recursive language. Let W and Z be two languages such that Y' reduces to W, and Z reduces to X' (reduction means the standard many-one reduction).
Which one of the following statements is TRUE ?
View solution
Q. Consider the following types of languages:
L1 Regular,
L2: Context-free,
L3: Recursive,
L4: Recursively enumerable.
Which of the following is/are TRUE?
I. L3' U L4 is recursively enumerable
II. L2 U L3 is recursive
III. L1* U L2 is context-free
IV. L1 U L2' is context-free
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Theory of Computation(TOC)? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!








