Question
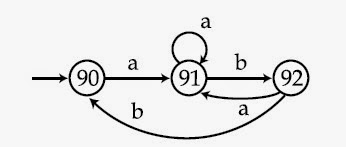
a.
Set of all strings containing ‘ab’
b.
Set of all strings containing ‘aab’
c.
Set of all strings ending in ‘abab’
d.
None of the above
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. The following deterministic finite automata recognizes:
Similar Questions
Discover Related MCQs
Q. The regular expression given below describes:
r=(1+01)*(0+λ)
View solution
Q. Which of the following language is regular?
View solution
Q. Which of the regular expressions corresponds to this grammar ?
S → AB / AS, A → a / aA, B → b
View solution
Q. Which of the following strings is in the language defined by grammar S→0A, A→1A/0A/1
View solution
Q. The logic of pumping lemma is a good example of:
View solution
Q. Let A = {x | -1< x< 1} = B. The function f(x)=x/2 from A to B is:
View solution
Q. Which sentence can be generated by S→d/bA, A→d/ccA:
View solution
Q. Regular expression a+b denotes the set:
View solution
Q. Which of the following is not true?
View solution
Q. Identify the language which is not context - free.
View solution
Q. The context-free languages are closed for:
(i) Intersection (ii) Union
(iii) Complementation (iv) Kleene Star
View solution
Q. Grammars that can be translated to DFAs:
View solution
Q. The language accepted by a Push down Automata:
View solution
Q. In parallel algorithm design, the process of grouping tasks into larger tasks in order to improve performance:
View solution
Q. Recursive Descent Parsers are a type of:
View solution
Q. If language L={0,1}*, then the reversed language L^R =
View solution
Q. Let r = a(a + b)*, s = aa*b and t = a*b be three regular expressions.
Consider the following:
(i) L(s) ⊆ L(r) and L(s) ⊆ L(t)
(ii) L(r) ⊆ L(s) and L(s) ⊆ L(t)
Choose the correct answer from given below:
View solution
Q. Consider the language L given by
L = {2^(nk) ∣ k>0, and n is non-negative integer number}
The minimum number of states of finite automaton which accepts the language L is
View solution
Q. The number of substrings that can be formed from string given by
a d e f b g h n m p
is
View solution
Q. Consider the following two languages:
L1 = {x ∣ for some y with ∣y∣ = 2^∣x∣,xy ∈ L and L is regular language}
L2 = {x ∣ for some y such that ∣x∣ = ∣y∣, xy ∈ L and L is regular language}
Which one of the following is correct?
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Theory of Computation(TOC)? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!


.png)





