Question
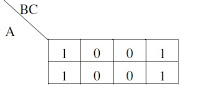
a.
A.B
b.
AB+BC+CA
c.
A.B.C
d.
None of the above
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. The function represented by the kmap given below is
Similar Questions
Discover Related MCQs
Q. The simplified form of the Boolean expression (X+Y+XY)(X+Z) is
View solution
Q. The answer of the operation (10111)2 * (1110)2 in hex equivalence is
View solution
Q. How many 1’s are present in the binary representation of
3 × 512 + 7 × 64 + 5 × 8 + 3
View solution
Q. The Boolean expression x’y’z+yz+xz is equivalent to:
View solution
Q. The octal equivalent of hexadecimal (A.B)16 is:
View solution
Q. The dual of the switching function x+yz is:
View solution
Q. The octal equivalent of the hexadecimal number FF is:
View solution
Q. The idempotent law in Boolean algebra says that:
View solution
Q. Simplified form of Boolean expression xy+(~x)z+yz is:
View solution
Q. In order to build a MOD-18 counter, the minimum number of flip flops needed is equal to:
View solution
Q. 2’s complement of -100 is:
View solution
Q. Which of the following expression remove hazard form: xy+zx’ ?
View solution
Q. How many 1’s are present in the binary representation of 15x256+5x16+3:
View solution
Q. If A⊕B=C, then:
View solution
Q. What is the maximum counting speed of a 4-bit binary counter which is composed of Flip-Flop with a propagation delay of 25ns?
View solution
Q. The hexadecimal equivalent of (10111)2 × (1110)2 is:
View solution
Q. An example of a self complementing code is:
View solution
Q. A sum of products expression can be implemented with...............logic gates.
View solution
Q. The number of 1’s present in the binary representation of (3x512 + 7x64 + 5x8 + 3)10 is:
View solution
Q. Which of the following expression removes static hazard from a two level AND-OR gate implementation of xy + zx’ ?
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Computer Arithmetic? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!




.png)



