Question
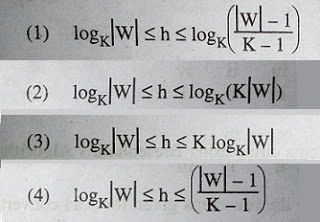
a.
1
b.
2
c.
3
d.
4
Engage with the Community - Add Your Comment
Confused About the Answer? Ask for Details Here.
Know the Explanation? Add it Here.
Q. Let G = (V,T,S,P) be a context-free grammar such that every one of its productions is of the form A→v, with |v| = K>1. The derivation tree for any W ϵ L(G) has a height h such that
Similar Questions
Discover Related MCQs
Q. Given the following two languages:
L1 = {a^nb^n|n≥0, n≠100}
L2 = {w ϵ {a,b,c}*| na(w) = nb(w) = nc(w)}
Which of the following options is correct?
View solution
Q. Given the following two statements:
A. L = {w|na(w) = nb(w)} is deterministic context free language, but not linear.
B. L = {an bn} U {an b2n} is linear, but not deterministic context free language.
Which of the following options is correct?
View solution
Q. Which of the following pairs have different expressive power?
View solution
Q. Which of the following statements is false?
View solution
Q. Let C be a binary linear code with minimum distance 2t + 1 then it can correct upto ............bits of error.
View solution
Q. From the given data below:
a b b a a b b a a b
which one of the following is not a word in the dictionary created by LZ-coding (the initial words are a, b)?
View solution
Q. The number of strings of length 4 that are generated by the regular expression (0+1+|2+3+)*, where | is an alternation character and {+, *} are quantification characters, is:
View solution
Q. Which of the following is FALSE ?
View solution
Q. The regular grammar for the language L = {a^nb^m | n + m is even} is given by
(A) S → S1 | S2
S1 → a S1 | A1
A1 → b A1 | λ
S2 → aaS2 | A2
A2 → b A2 | λ
(B) S → S1 | S2
S1 → a S1 | a A1
S2 → aa S2 | A2
A1 → bA1 | λ
A2 → bA2 | λ
(C) S → S1 | S2
S1 → aaa S1 | aA1
S2 → aaS2 | A2
A1 → bA1 | λ
A2 → bA2 | λ
(D) S → S1 | S2
S1 → aa S1 | A1
S2 → aaS2 | aA2
A1 → bbA1 | λ
A2 → bbA2 | b
View solution
Q. Let Σ = {a, b} and language L = {aa, bb}. Then, the complement of L is
View solution
Q. Consider the following identities for regular expressions :
(a) (r + s)* = (s + r)*
(b) (r*)* = r*
(c) (r* s*)* = (r + s)*
Which of the above identities are true ?
View solution
Q. Given the following two languages:
L1 = {uww^Rn | u, v, w ϵ {a, b}+}
L2 = {uwwR^n | u, v, w ϵ {a, b}+, |u| ≥ |v|}
Which of the following is correct ?
View solution
Q. Given a Turing Machine:
M = ({q0, q1}, {0, 1}, {0, 1, B}, δ, B, {q1})
Where δ is a transition function defined as
δ (q0, 0) = (q0, 0, R)
δ (q0, B) = (q1, B, R)
The language L(M) accepted by Turing machine is given as :
View solution
Q. Consider the following linear programming problem:
Max. z = 0.50x2 – 0.10x1
Subject to the constraints
2x1 + 5x2 ≤ 80
x1 + x2 ≤ 20
and x1, x2 ≥ 0
The total maximum profit (z) for the above problem is:
View solution
Q. The regular expression for the complement of the language L = {anbm|n≥4, m≤3} is:
View solution
Q. Consider the following two languages:
L1 = {0i1j | gcd(i,j)=1}
L2 is any subset of 0*.
Which of the following is correct?
View solution
Q. Let L be the language generated by regular expression 0*10* and accepted by the deterministic finite automata M. Consider the relation RM defined by M. As all states are reachable from the start state, RM has ................ equivalence classes.
View solution
Q. Let L = {0^n1^n | n≥0} be a context free language.
Which of the following is correct?
View solution
Q. Given a Turing Machine
M = ({q0,q1,q2,q3}, {a,b}, {a,b,B}, δ, B, {q3})
Where δ is a transition function defined as
δ(q0,a) = (q1,a,R)
δ(q1,b) = (q2,b,R)
δ(q2,a) = (q2,a,R)
δ(q2,b) = (q3,b,R)
The language L(M) accepted by the Turing Machine is given as:
View solution
Q. Match the following :
List - I List - II
(a) {a^n b^n|n > 0} is a deterministic (i) but not recursive language
context free language
(b) The complement of {a^n b^n a^n|n > 0} (ii) but not context free language
is a context free language
(c) {a^n b^n a^n} is context sensitive language (iii) but can not be accepted by a deterministic pushdown automation
(d) L is a recursive language (iv) but not regular
Codes :
(a) (b) (c) (d)
View solution
Suggested Topics
Are you eager to expand your knowledge beyond Theory of Computation(TOC)? We've curated a selection of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of Computer Science. Happy exploring!
.png)







